Documentation/Nightly/Modules/BrainLogisticSegmentation
|
For the latest Slicer documentation, visit the read-the-docs. |
Introduction and Acknowledgements
|
Extension: Brain Tissues Extension | |||||||
|
Module Description
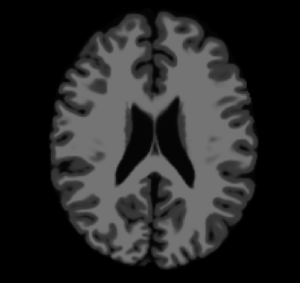
This CLI module offers the Brain Logistic Segmentation (BLS) algorithm, which is a fully automatic segmentation method for MRI structural images. Although the method was intensively tested over T1 weighted (T1w) MRI images, it could be also applied to similar structural MRI data such as T2w and PDw images. The only requirement that is needed in BLS method is that the image histogram can be enough information to describe each tissue of interest (defined as distinguished peaks at image histogram). A full description of BLS method can be found at the paper published at ... journal (DOI: ).
NOTE: A small set of pre-processing steps are usually required for a smooth tissue segmentation using BLS. Methods such as image denoising (e.g. Anomalous Filters) and bias field correction (N4 ITK Bias Field Correction) can greatly assist to the BLS convergence.
Use Cases
- Use Case 1: General brain tissue segmentation
- There are several image quantitative approaches that use only a certain tissue type (for instance, cortical thickness) in which a previous brain segmentation could be needed.
- Use Case 2: Brain extraction refinement
- In some occasions, the brain extraction procedure may leave non-brain tissues on the final brain mask (e.g. dura). Using a simple brain tissue mask offered in BLS method can be helpful to remove undesired non-brian information on further analysis (e.g. cortical thickness, total intracranial volume and brain atrophy).
Panels and their use
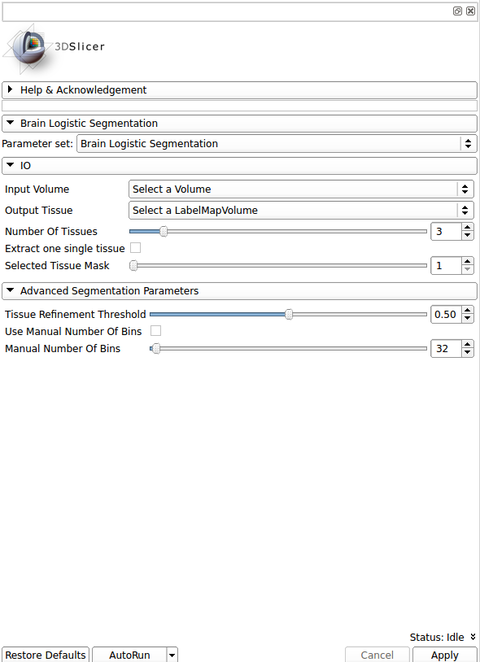
IO:
- Input Volume
- Input volume (T1, T2 or PD MRI images)
- Output Tissue
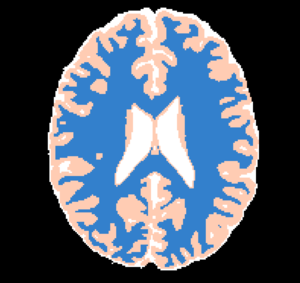
- Output Tissues. A binary mask with all the tissues being represented
- Number Of Tissues
- The number of tissues presented in the input image. This should be driven by the image histogram peaks.
- Extract one single tissue
- Choose this if you want a single tissue as the output mask.
- Selected Tissue Mask
- Select what tissue that should be exported. Here the order is always given from the brightest to darkest tissue. For instance, for T1 images, the white matter is 1, gray matter is 2 and CSF is 3.
Advanced Segmentation Parameters:
- Tissue Refinement Threshold
- Defines the logistic classification threshold that should be adopted in order to define the binary mask. If thr=0.5, all the tissues are precisely added without any overlay. If thr<0.5, there is a tissue mask overlay representing the partial volume (PV) among tissues, which is placed in an additional tissue mask (PV masking). If thr>0.5, the overlay is also presented regarding PV, however, the output is changed to zero, i.e. the overlying tissue is not represented as an additional mask.
- Use Manual Number Of Bins
- Choose if you want to set the number of bins manually.
- Manual Number Of Bins
- Define the number of bins.
Similar Modules
References
- paper
Information for Developers
| Section under construction. |