Difference between revisions of "Modules:MeshContourSegmentation-Documentation-3.6"
| Line 51: | Line 51: | ||
| | | | ||
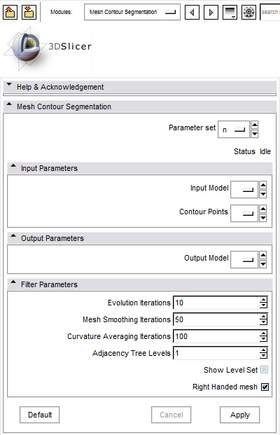
* '''Input panel:''' | * '''Input panel:''' | ||
| − | + | Input Model: PolyData for input | |
| − | + | Contour Points: Fiducial List to input (Must be "Selected" in Fiducials Module) | |
| − | + | Output Model: The PolyData into which to put the result | |
| − | + | ||
| − | + | Evolution Iterations: Number of Levelset Iterations | |
| − | + | Mesh Smoothing Iterations: Number of times to pre-smooth the mesh for better geometry computation | |
| − | + | Curvature Averaging Iterations: Number of times to average computed mean curvature and gradient, to make evolution smoother | |
| − | + | Adjacency Tree Levels: How deep of a neighborhood lookup to build. If the mesh is very fine and practically 'flat' everywhere, this must increase. Exponentially slows things down as it is raised (Suggestion: make the mesh as coarse as practical so it can be set to 1 or 0) | |
| − | + | Right Handed Mesh: whether the normal vector needs a negative sign or not. | |
|[[Image:Sfls_interface.png|thumb|280px|User Interface]] | |[[Image:Sfls_interface.png|thumb|280px|User Interface]] | ||
|} | |} | ||
Revision as of 21:10, 2 May 2010
Home < Modules:MeshContourSegmentation-Documentation-3.6Return to Slicer 3.6 Documentation
Mesh Contour Segmentation
MyModule
General Information
Module Type & Category
Type: CLI
Category: Segmentation
Authors, Collaborators & Contact
- Peter Karasev (Author): Georgia Tech
- Karol Chudy (Author): Georgia Tech
- Allen Tannenbaum (Collaborator): Georgia Tech
- Contact: Peter Karasev, pkarasev@gatech.edu
Module Description
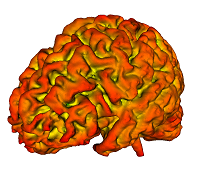
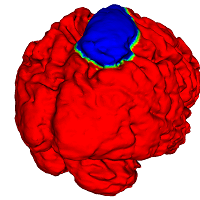
This module is a tool to generate closed contours on a surface in 3D. The contour is initialized with a set of points, and subsequently 'evolves' according to some geometric criterion of the underlying surface (e.g. Surface Normal, mean curvature, second fundamental form, etc) and the embedded curve (e.g. geodesic & normal curvatures, etc ).
The implementation uses a version of Sparse Field Level Sets (Whitaker et al 1998) modified for a mesh where there is an arbitrary number of vertex neighbors.
While the motivating problem is segmentation of Sulci & Gyri on the cortical surface, the technique is also applicable to analysis of other anatomic structures (e.g. bones and fractures thereof).
Usage
Use Cases, Examples
1. Compute & Display surface mean curvature, when noise in the mesh precludes the ITK function of similar purpose from producing good result:
2. Mark and Display segment of the surface in virtual colonoscopy, e.g. to mark a tumor location
Tutorials
- Load the scene in the below data set. You will see 6 fiducial points as initializers. Select the module from Modules -> Segmentation -> MeshContourSegmentation. Create a new output model, and apply. It will take a few minutes, due to geometry computation across the entire large mesh.
- Media:Meshexample-2010-04-23.zip
Quick Tour of Features and Use
A list panels in the interface, their features, what they mean, and how to use them. For instance:
Input Model: PolyData for input Contour Points: Fiducial List to input (Must be "Selected" in Fiducials Module) Output Model: The PolyData into which to put the result Evolution Iterations: Number of Levelset Iterations Mesh Smoothing Iterations: Number of times to pre-smooth the mesh for better geometry computation Curvature Averaging Iterations: Number of times to average computed mean curvature and gradient, to make evolution smoother Adjacency Tree Levels: How deep of a neighborhood lookup to build. If the mesh is very fine and practically 'flat' everywhere, this must increase. Exponentially slows things down as it is raised (Suggestion: make the mesh as coarse as practical so it can be set to 1 or 0) Right Handed Mesh: whether the normal vector needs a negative sign or not. |
Development
Notes from the Developer(s)
- Give it some seed points for initialization.
- Seed points do *NOT* need to be 'in order', but of course the closer they are to the expected final result, the better.
- The region being marked as initial should be convex.
- The initial contour is formed like this: connect all seed points to eachother, and fill the convex hull. The boundary of this convex fill is the initial contour.
- Slow part of the computation: forming adjacency tree for curvature computation. The parameter "adjacency levels" says how many levels to branch out from each vertex when fitting paraboloid. These neighbors are stored, because they are needed when computing the curve geometry during levelset evolution.
- Output: MeanCurvature is scaled to [-256,256] and displayed everywhere. The ActiveContourVertices array gives the location of segmented region on the mesh.
Dependencies
Other modules or packages that are required for this module's use:
-Only VTK & STL
Tests
On the Dashboard, these tests verify that the module is working on various platforms:
http://www.cdash.org/CDash/testDetails.php?test=52059394&build=600130
Known bugs
Links to known bugs in the Slicer3 bug tracker
Usability issues
Follow this link to the Slicer3 bug tracker. Please select the usability issue category when browsing or contributing.
Source code & documentation
Links to the module's source code:
Source code:
Several Key Points:
- Entry Point from Slicer
- Computation of Initial Path from Un-Ordered Initial Points
- Adjacency Tree, Mean Curvature, Curvature Surface Gradient Computation
- Levelset Evolution Entry Point
- Levelset Evolution Core
Doxygen documentation:
More Information
Acknowledgment
This work was supported in part by grants from NSF, AFOSR, ARO, as well as by a grant from NIH (NAC P41 RR-13218) through Brigham and Women’s Hospital. An NSF Fellowship supported part of the work.
References
P.A. Karasev, J.G. Malcolm, M. Niethammer, R. Kikinis, A. Tannenbaum. User-Driven 3D Mesh Region Targeting. To appear in SPIE Medical Imaging 2010.